【知识探索】影响先进半导体的核心技术——从对称性的角度观察半导体外延晶体生长 第一章

1.引言

        近年来，半导体技术的重要性被再次提出，而作为基础材料的半导体晶体制备技术，更是不可或缺的核心技术。人们通常会直接将“半导体”与半导体芯片联系起来，但在确保半导体芯片的性能方面，提升作为基础材料的半导体晶体质量尤为重要。无论是光学器件还是电子器件，其性能都基于半导体材料“晶体”的特性。通过充分利用晶体的特性，才能发挥出半导体芯片的最大性能。从原子层面来讲，“晶体”是指具有特定单元结构（称为“晶胞”）并在空间中规则排列（换句话说，是具有平移对称性）的固体。对于半导体晶体来说，其特性在很大程度上受到晶体内部规则性的影响。由于半导体晶体需要通过消除各种有损于规则性的晶体缺陷来增强其完整性。因此，毫不夸张地说，能实现完美结晶的半导体晶体制造技术是作为先进半导体的核心技术。

        在制备实际使用的各种尺寸的大型晶体时，理想状态是晶体全区域都保持完美性（即晶胞的平移对称性贯穿整个晶体）。但在实际的晶体生长过程中，通常会出现微小晶粒的聚合现象。在这种情况下，实现晶体的“规则排列”是半导体晶体工程学所追求的终极目标。然而，在晶粒边界区域，往往因为难以维持平移对称性（即在六面体的平行移动下无法与相邻的六面体重叠），导致晶体缺陷的产生。或者在长晶过程中由于晶体缺陷的发生导致平移出现中断。随着晶体生长的进行，缺陷会逐步传播，甚至延伸至表面，最终影响半导体芯片的性能，尤其是在初始性能和长期可靠性方面。

        从半导体晶体的角度回顾半导体技术的发展历程，最初以锗（Ge）开始，随后硅（Si）技术取得了巨大进展。如今，硅方面已经实现近乎完美的晶体，这些高质量的大尺寸硅晶体广泛应用于当前的主流半导体技术中的大规模集成电路（LSI）。然而，由于硅材料在性能提升方面存在局限性，特别是在光学器件和高频应用领域，人们开始研究以砷化镓（GaAs）为代表的III-V族化合物半导体，并且这些材料逐渐得到了应用。随后，随着短波长光学器件和功率应用的需求增加，氮化镓（GaN）和碳化硅（SiC）等宽禁带半导体开始受到关注，并逐步研发出基于这些材料的半导体器件。当前，在功率应用领域，氧化镓（Ga₂O₃）、氮化铝（AlN）以及金刚石半导体的开发也在稳步推进，拓宽了功率应用的领域。

        从晶体结构的角度重新审视上述半导体材料的发展历程，不难发现其中一些有趣的特点。最早的Ge和Si属于元素半导体，具有金刚石结构的晶体。随后出现的GaAs等III-V族化合物半导体虽然是二元化合物，但其结构类似于Si的闪锌矿结构，这些材料具有较高对称性的立方晶系结构。而之后的GaN和SiC则主要为六方晶系结构的纤锌矿型晶体。再后来出现的Ga₂O₃，则呈现出与之前材料显著不同的三方晶系的刚玉结构，或是单斜晶系的晶体。

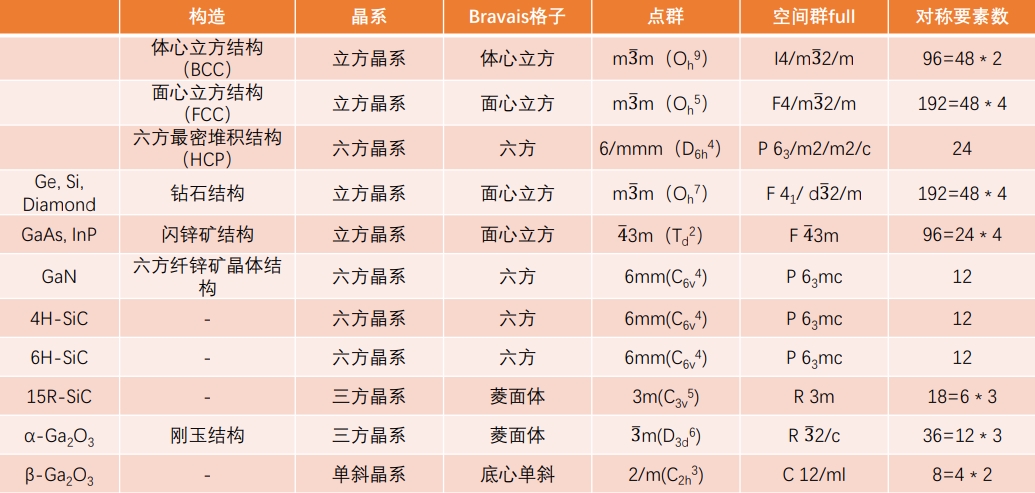
表 1-1 各种半导体材料的晶体结构

        这些半导体材料的晶体结构如表1-1所示（具体细节将在后文中讨论），其中既有相对简单的结构，也有相当复杂的结构。这里，我们以一个粗略的比喻来说明，想象一下将具有晶系特有单元格形状的多个平行六面体（下文简称为“六面体”）装入一个盒子的过程（见图1-1）。如果将许多六面体杂乱无章地放进盒子里，很难让它们排列整齐。然而，如果通过摇晃盒子等方式给予外部刺激，虽然不一定完全整齐，但可以达到一定程度的规则排列。并且，如果这些六面体的形状类似于骰子那样的立方体，排列起来会更加容易（反过来说，如果六面体形状不规则，则更难排列）。

        此外还可以考虑这样一种情况，如图1-2所示，可以设想在规则排列的六面体（晶体）中，将其中一个六面体取出，经过旋转改变其姿态后重新放置。如果是立方体，即使围绕特定轴旋转90°，其顶点会互相交换，但整体的空间坐标轴（图中的x、y、z轴）相对的位置不会改变，因此可以直接将其以原姿态重新融入晶体。然而，对于一般的六面体，即便进行相同的旋转操作，也无法直接重新融入晶体。

        由此可以推测，如果六面体具有像立方体那样的高对称性（比如从形象上理解为“8个顶点没有差别”），它们会更容易排列成规则的结构。这种直观的想法或许可以帮助我们理解晶体排列的规律性。

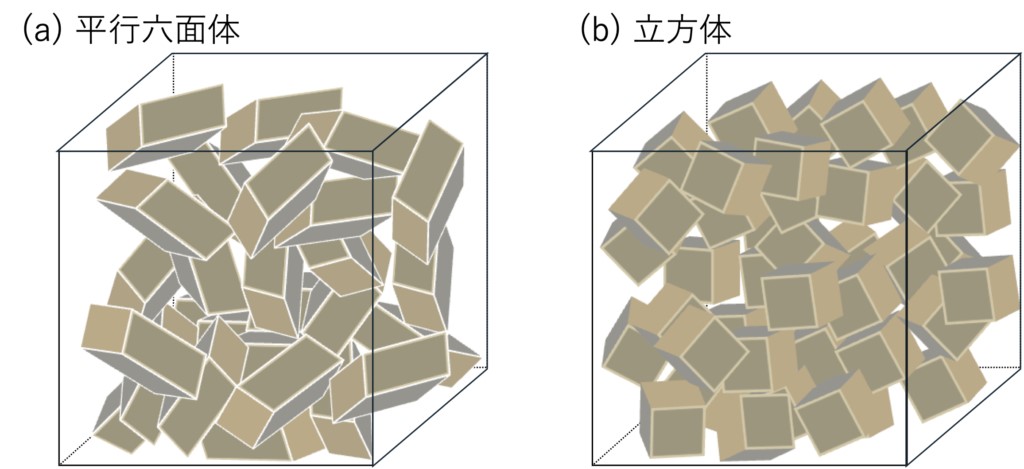
图 1-1 平行六面体装箱示意图。

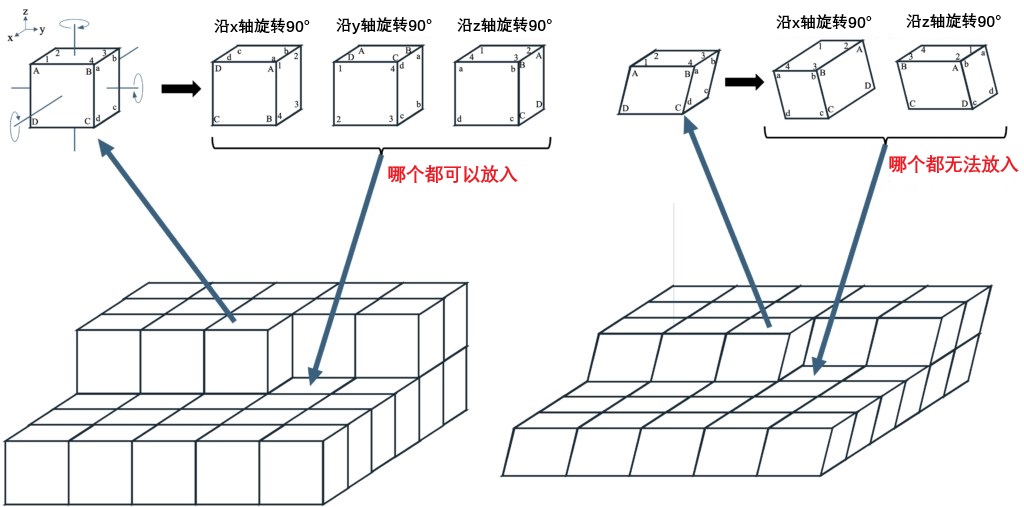
图 1-2 将平行六面体进行有规则的三维排列的过程。 如果是立方体，在进行旋转操作后，它的方向不会改变，可以有规则地排列，但一般的平行六面体在进行类似的旋转操作后，其方向无法有规则地排列。

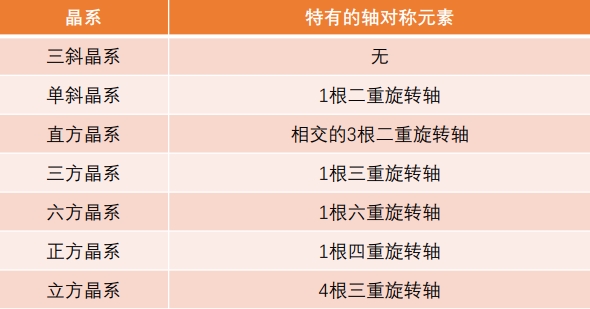
        图1-3显示了六面体和立方体的部分对称元素。例如，在旋转对称性方面，立方体具有四重对称轴或三重对称轴，而六面体只有反转中心。换句话说，相较于六面体，立方体更容易保持相同的姿态，从而更容易实现规则排列。也就是说，当晶体的单元格对称性较高时，它们能够更好地填满三维空间，同时保持平移对称性，这意味着可以形成无缺陷的完全晶体（即没有缺陷的完美晶体）。每种材料的晶体结构都由以下几个对称元素的组合特征化：用于表达单元格对称性的“布拉维格子（Bravais格子）”、代表格点上“基本要素”对称性的点群、以及由Bravais格子和点群组合形成的“空间群”。首先，我们可以考虑格子所表达的单元格对称性是否适合填满空间（即平移群的问题）。其次，还可以考虑基本结构的对称性及化学键的方向性（即点群的问题）对单元格排列的影响。空间群所拥有的对称元素的数量可能成为衡量对称性优劣的一个指标。本文将通过大量的图示，围绕这些半导体材料之间的共性和差异性，从晶体的对称性（即晶体是否在平移或旋转操作下能够完全重合）以及外延生长过程中伴随的晶体缺陷发生的角度进行通俗易懂的比较，并融入一些独特的视角。换个角度来说，这是一种在三维空间中像搭积木一样的讨论方式，希望读者能够轻松地阅读下去。在第（2）部分中，将讨论立方晶体；第（3）部分将介绍六方晶体；第（4）部分将讨论其他类型的晶体，最后进行总结。

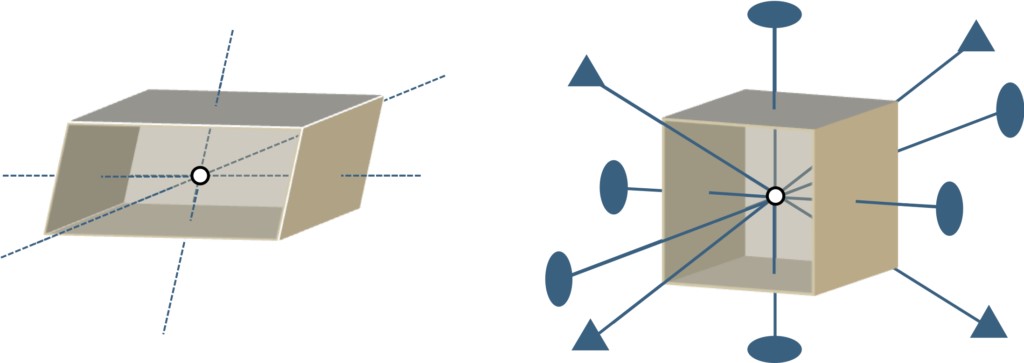
图1-3一般情况下关于六面体和立方体的对称性图示。

·表示两重旋转轴，▲ 表示三重旋转轴，○ 表示反转中心。

        晶体学特有术语和基本概念的解释因过于繁琐而未在文中详述，但已在文章末尾的附录（Appendix 1、2、3）中列出，详情请参考附录。另外，虽然为了全面理解现象，可能还需要从能量的角度进行考量，但本文的讨论仅限于形态学方面的晶体学讨论，还请谅解。

2.晶体生长与晶体的对称性

        接下来，在实际晶体的生长过程中，晶体的对称性是如何维持的呢？让我们重新审视一下晶体生长的含义。为了让作为晶体原料的微小原子团成长为宏观尺度的固体晶体，首先需要这些“点”状的原子团以某种方式聚合在一起。在所谓的“无籽晶生长”中，最初会发生自然核形成，这可以理解为原子团在自由空间中无特定方向地聚合。然而，除非是无定形结构，否则即使是自然形成的核，在微观范围内也应保持结晶的对称性。而一旦具有晶体特性的自然形成核达到一定的尺寸，随后的生长可以理解为沿某一晶面上的生长（在顶点或边缘上生长的可能性很小）。因此，接下来的讨论将假设“有籽晶生长”情况下作为衬底的晶体，并将讨论晶体在基底晶体表面特定晶面上的生长。

        在二维表面上的晶体生长中，下层衬底的晶体结构信息传递至上层生长层的薄膜生长现象被称为外延生长（Epitaxial Growth）。在微观层面上，已知外延生长主要有以下三种方式：

        （1）岛状生长（Volmer-Weber 型）

        （2）层状生长（Frank-von der Merwe 型）

        （3）复合生长（Stranski-Krastanov 型）

图 1-4 外延生长的生长模式。 第一行表示少于 1 个原子层的总生长，第二行表示 1-2 个原子层，第三行表示超过 2 个原子层。

        这些情况在图1-4中有所展现。为了实现理想的外延生长，(2) 层状生长是必不可少的，之后再通过层层叠加形成完整的晶体。然而，在大到晶圆级别的宏观尺度上完全实现 (2) 的层状生长是极其困难的。即使能够准备如图1-4所示的完全平坦的晶体衬底表面，在衬底上的某一区域可能会形成“区域A”（Domain A），而在另一区域则会形成不同的“区域B”（Domain B）。尽管在区域内可能实现了层状生长，但在宏观尺度上仍会形成岛状的区域。这是因为即使是初始的晶体衬底，在原子层级别上也不可能完全平整，往往会产生原子层级的台阶（step）。尽管生长出来的两个区域在物质和结构上应与衬底上的外延生长层相同，但随着生长的进行，这两个区域在某处地方会发生碰撞。图1-5图示了这种情况，由于岛状区域的起点在Domain A和B有所不同，因此在这一过程中，Domain A和B之间不会存在如外延结构的直接传播关系。在理想情况下，如果衬底的结构信息能够准确地传递到Domain A和B，那么即使A和B发生碰撞，其间的晶体平移对称性依然可以得到保持，从而形成一个完整的单一晶体。然而，如果在层状生长过程中其中一个区域出现了某种晶体生长上的“错误”，则无法保证Domain A和B具有相同的对称性，这可能会导致合并边界处晶体的平移对称性被破坏。此外，衬底的应变等因素可能导致两个域的晶体轴发生细微的偏移。在这种情况下，合并边界会成为一种晶体的缺陷。

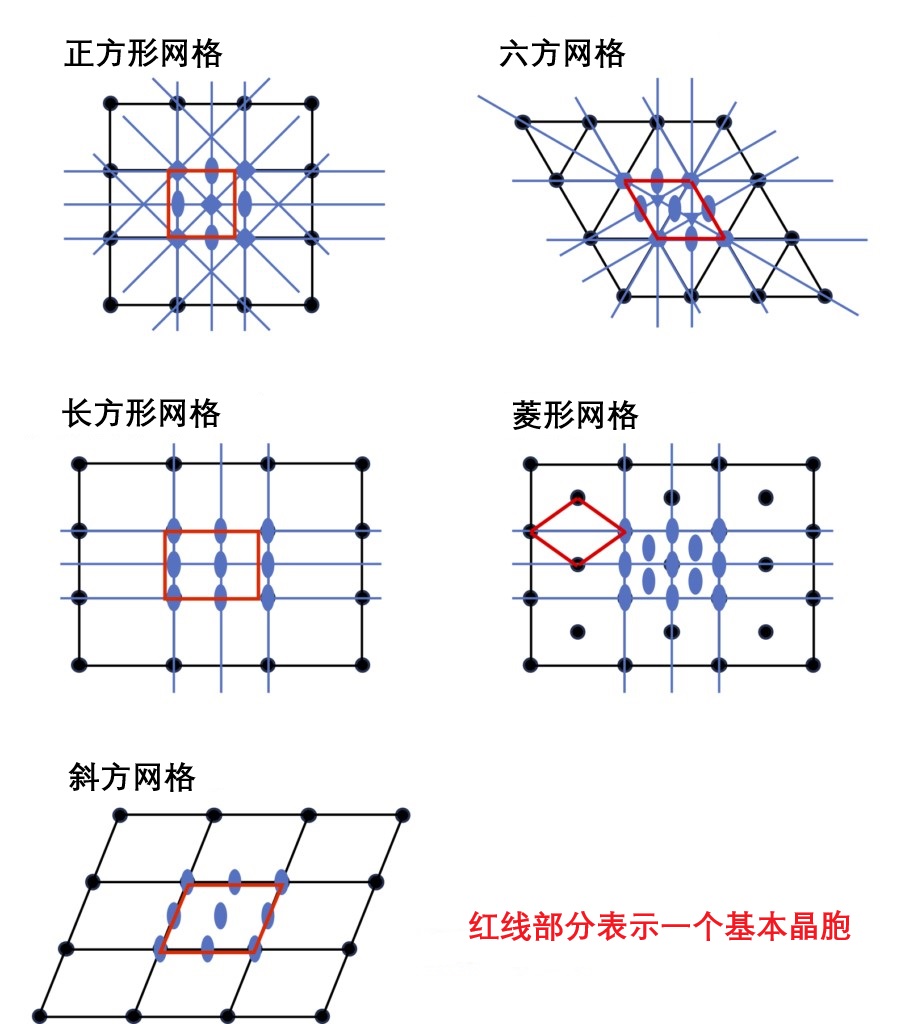
图 1-5 实际外延生长过程中不同生长区域的碰撞。

        在外延层状生长过程中，所堆叠的层所传递的结构信息，基本上来源于下方衬底的表层。通过在堆叠过程中逐层传递这一表层的结构信息（包括对称性），从而形成了三维的结晶体。简单来说，这里层的对称性相当于“通过平移能完全重叠的壁纸”的对称性，这种对称性在二维平面群（准确地说，是存在正反面的“layer group”，详见《国际晶体学表》Volume E）中被系统地总结。这一“layer group”信息逐层堆叠后可以理解为转变成了三维的“空间群”。但是，由于层群本身并不包含堆叠方向的信息，因此在堆叠过程中会与原本晶体结构所具有的空间群不完全匹配，这种不匹配便是前述晶体生长过程中出现“错误”的本质原因。与三维晶体结构一样，二维的层结构也可以用“晶格 + 基本要素”来表示。因此，在接下来的讨论中，我们将频繁使用的二维平面中的二维网格（晶格）在图1-6中进行了展示。它们对应于三维空间中的Bravais格子，并且如图所示，分为五种类型。

图 1-6 表示二维平面晶格结构的各种二维网及其对称元素。

        作为连续系列文章的第一部分，本文从晶体对称性的角度介绍了在半导体材料外延生长过程中的问题与考察。接下来的内容，将结合实际的半导体晶体生长实例，逐一介绍各类半导体材料的晶体结构特点、共性与差异，还将对晶体结构和生长层的对称性对外延生长的影响进行比较分析。

参考文献

1. “物質の対称性と群論”: 今野豊彦（共立出版, 2001）
2. “Int. Tables for Crystallography, Volume A, 6th edition”: Eds. M.I. Aroyo (Wiley, 2016)、 On-line版はhttps://it.iucr.org/services/purchase/
3. “Int. Tables for Crystallography, Volume E, 2nd edition”: Eds. V. Kopsky and D.B. Litvin (Wiley, Dec. 2010)

附录（Appendix 1）

        在讨论晶体对称性时，以下信息为基本所需。

        · 格子

        在晶体中，具有相同周围环境的位置可以用点来表示，这些点称为格子点，而格子点的集合就是格子。格子点的选择具有一定的任意性，原子不一定总是出现在格子点上。此外，整个格子可以表示为由格子点构成的合适的平行六面体的集合，这个平行六面体称为晶胞（Unit Cell）。晶胞的选择也具有一定的任意性，但通常选择对称性尽可能高的晶胞。在所有晶胞中，体积最小且包含一个格子点的晶胞（其中边或顶点上的格子点被分割到多个晶胞中）称为基本晶胞。为了表示平行六面体，可以将一个顶点相连的三条边当作向量，从该顶点开始分别定义为a轴、b轴和c轴（标准为右手系）。与a轴、b轴、c轴对应的向量（平移向量）的长度称为a, b, c，其夹角分别称为α, β, γ，这些参数统称为格子常数。任意格子点之间的向量称为平移向量，将平移向量的整数倍也视为平移向量。表示基本晶胞三边的向量称为基本平移向量。

        · 基本要素（Motif）

        在晶体中，配置在格子点处的原子等（包括原子、离子或分子）的集合称为基本要素。在讨论对称性时，合理定义基本要素的范围及其相对于格子点的位置非常重要。基本要素可以由其中某一点的周围对称性来描述。

        · 晶体结构

        晶体结构是对晶体内部原子等的排布描述。晶体结构可以通过定义格子和配置在所有格子点上的基本要素（原子等的集合）来表示。即：

        晶体结构 = 格子 + 基本要素（Motif）

        在晶体中，基本平移向量所定义的平移对称性及格子点周围的对称性得以保持，晶体结构就是以这种对称性为特征的。

        · 格子结构

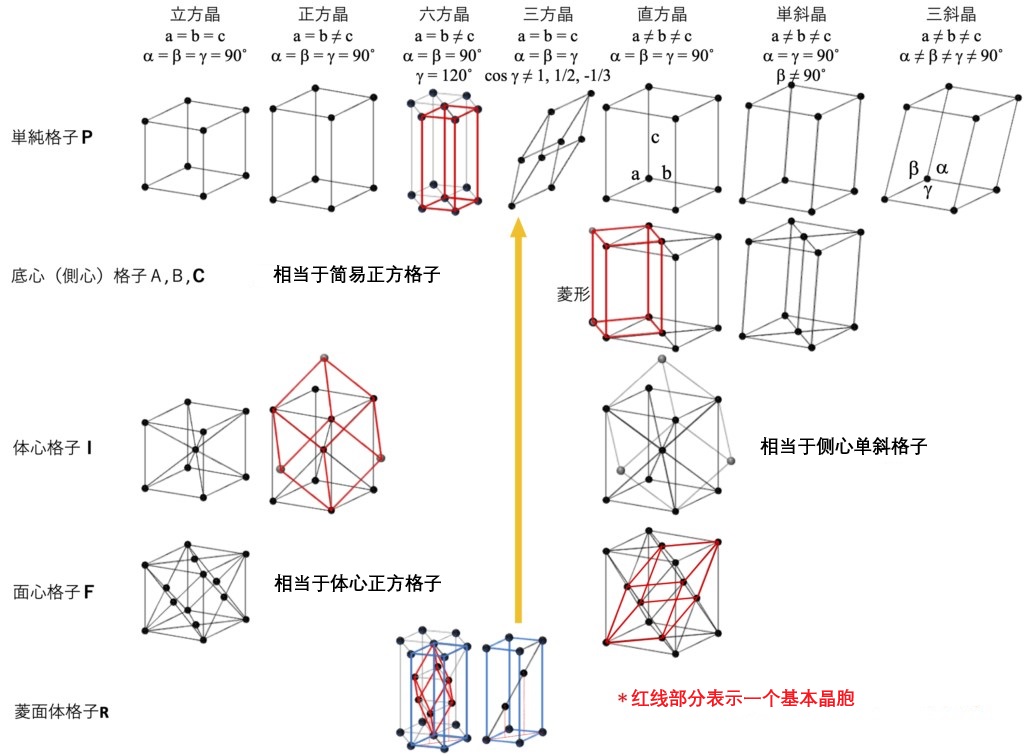
        格子结构是由构成它的格子点的排列决定的。最基本的是简易格子，即平行六面体。为了保持平移对称性，简易格子可以通过平行移动（称为中心化）来与其他简易格子结合，这种移动后的格子称为副格子。为了更直观地表达，格子通常被组合成复合格子，方便人们理解。复合格子有四种类型：体心晶格、面心晶格、底心（侧心）晶格和斜方晶格。 如果单位胞是复合格子，虽然对称性降低，但可以分解为体积更小的基本单位胞。在复合格子中，通常将复合格子本身作为单位胞，而不是基本单位胞，并通过定义其三个向量来确定格子常数。下面将展示各复合格子中的副格子的数量及其移动量。

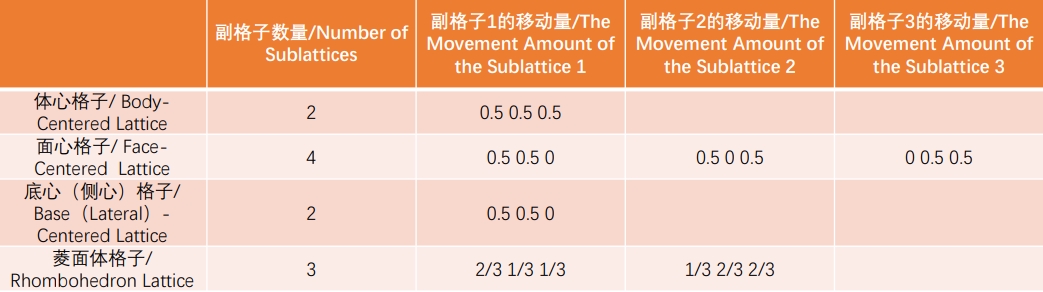
上述移动量为将各晶轴的长看作1后得出的概念值

        · 格子的对称性与晶体系、Bravais格子

        根据格子的对称性（a, b, c, α, β, γ 的关系），格子可以被分类为七种晶体系：三斜晶系、单斜晶系、直方（斜方）晶系、正方晶系、六方晶系、三方晶系和立方（等轴）晶系，每一种都具有特有的结晶点群对称操作。通过格子类型和晶系的组合，除了等效的情况，导出十四种称为Bravais格子的格子（见下图）。如六方晶的简易格子中的六角柱图示说明，这不是复合格子或（基本）单位胞。菱面体格子可以作为简易六方格子的复合格子来表示，但通常会将其作为一个与基本单位胞不一致的、易于理解的四棱柱（由红线表示）的三方晶系。对于简易三方格子，当γ有特定的特殊值时，会变成一个对称性更高的其他Bravais格子。例如，cos γ = 0（γ = 90˚）时为简易立方格子，1/2（γ = 60˚）时为面心立方格子，-1/3（γ = 109.47˚）时为体心立方格子。在单斜晶系中，有时会将γ ≠ 90˚视作一种惯例，而在某些情况下，也可以选择β ≠ 90˚。在下图中，β ≠ 90˚为默认选择，展示了各晶体系特有的对称元素。