

【知识探索】影响先进半导体的核心技术——从对称性的角度观察半导体外延晶体生长 第二章
日期:2025-03-18阅读:3916
导读
《知识探索》是公众号全新推出的科普专栏,专注于前沿材料与基础科学的深度解析。将聚焦“氧化镓”这一新兴半导体材料,从晶体结构、物理特性到应用场景,带您全面了解其在 5G 通信、新能源汽车等领域的突破性潜力。同时,栏目还将探讨氧化物材料的科学原理,揭示其在能源、环保、电子等领域的广泛应用。
在上一篇文章中,我们从晶体对称性的角度概述了各种半导体晶体的特征及其关联性。本篇将基于 HCP 的六方晶和三方晶进行讨论。我们首先阐述六方晶系和晶系之间的对应关系,并概述斜方晶格、立方晶格之间相互的关系。然后,我们将从对称性的角度比较基于 HCP 的晶体结构的细节,并探讨缺陷产生的差异。
作者简介

本文作者奥村元,工学博士(大阪大学)。现担任有限责任合伙“Innovative Semiconductors, Electronics & Energy Solutions”代表人,日本国立产业技术综合研究所名誉研究员,日本筑波大学名誉副教授。
六方晶系和三方晶系
在讨论晶系时,六方晶系和三方晶系的区分经常引起混淆。六方晶系和三方晶系的本质区别在于晶体的对称性,即六方晶系具有 6 条对称轴(旋转、反转、螺旋),而三方晶系具有 3 条对称轴。事实上,这两种晶系的格子结构是相同的,如图 2-1 所示,二维的六方网格垂直于平面堆叠,就形成了六方格子(用晶格常数表示为a = b ≠ c,α = β = 90°,γ = 120°)。由于 60° 旋转两次等于 120° 旋转,因此三方晶系似乎包含在六方晶系中(实际上,由于平移对称性,当形成格子时两者相同),但是当将基本结构的点群对称性设为 3 次旋转轴时,整体的对称性就变为 3 次旋转轴。图2-2显示当六方网格的格点上存在 6 次旋转轴和 3 次旋转轴时,六方网上出现的对称元素。从该图可以清楚地看出对称性的差异。虽然 (2/3, 1/3, 0) 和 (1/3, 2/3, 0) 位置的基本单元格中都出现了 3 次旋转轴(红框所示),但在 (1) 中,基本单元格的中心和边上出现了 2 次旋转轴。此外,(1) 中还增加了 {1-10} 面的镜面。
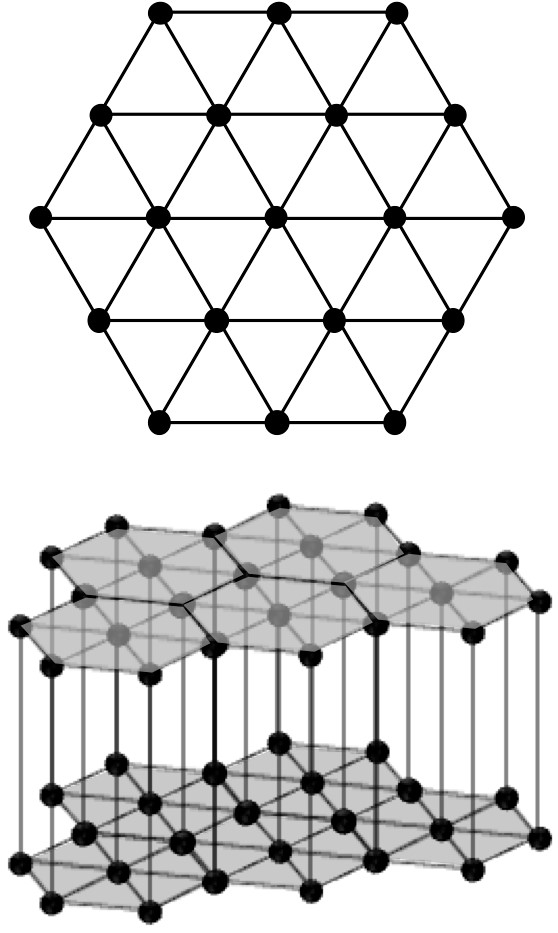
图 2-1 六方网格点和六方格子
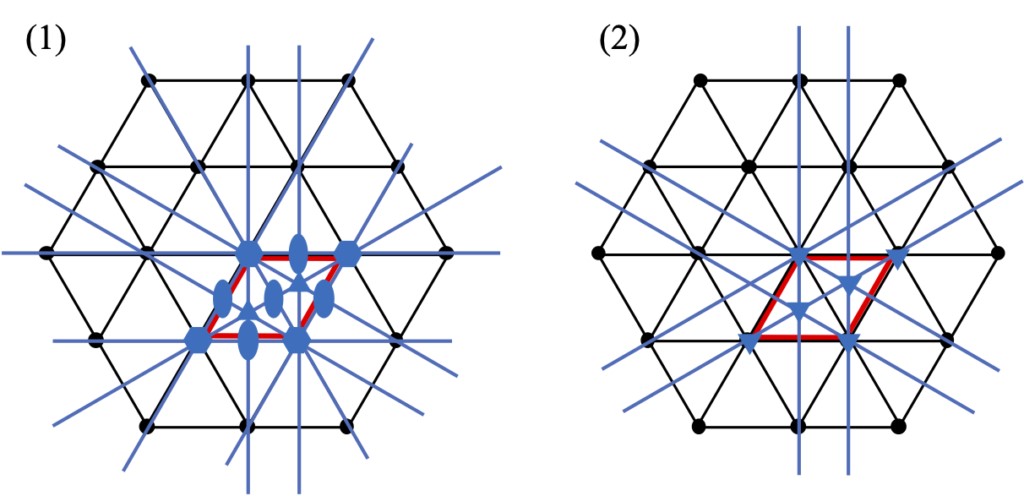
图 2-2 (1) 六方晶系对称要素;(2) 三方晶系对称要素和六方网格。红色方框是六方网格的基础单元格。
现在,让我们重新观察斜方格子、六方格子以及HCP结构之间的关系。图 2-3 展示了常见的 HCP 结构中原子最密堆积的排列。粗黑框是基础六方格子的基本单元格。黑点和红点表示原子。在该图中,基础六方格子的格点被定义为与黑点原子位置重合。红点的位置乍一看似乎也是格点,但实际上并非如此。根据格点的定义,连接格点之间的向量(平移向量)的整数倍也应该是平移向量,但是如果将红点的位置也作为格点,那么如图中红箭头所示,连接左下角黑点格点与红点的位置的向量,其两倍的位置上并没有格点。
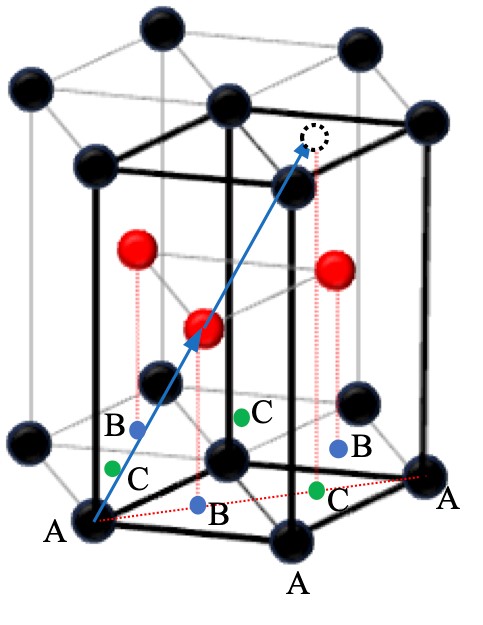
图 2-3 HCP 结构。粗体黑框是其基本单元格。
那么,如果将图 2-3 中红点和白点的位置作为格点,整个格子的结构应该是什么样的呢?重新绘制后的结果如图 2-4 (1) 所示。换句话说,如果将图 2-3 中蓝箭头的位置、及其两倍和三倍的位置作为格点,并在这些位置上也放置原子,就可以与平移对称性相协调。这种格子如图 2-4 (2) 和 (3) 所示,是由三个基础六方格子组成的复合格子,称为斜方格子。在这种情况下,层与层之间的间距(c 轴长度的 1/3)在格子结构上没有特殊的限制,只有红点在 a-b 平面内的位置是重要的。然后,将三个斜方格子以120°的间隔旋转放置在通常绘制的六棱柱中,就可以重新构建如图 2-4(4) 所示的基本平移向量。这就是基础的三方格子。也就是说,将简单六方格子向 (1/3, 1/3, 1/3) 和 (2/3, 2/3, 2/3) 平移(以图 2-4(3) 的左下角格点为原点)得到的副格子与之结合,从复合格子的基本平移向量重新构建得到的简单格子,就是作为三方晶系处理的简单三方格子。三方格子可以用六方格子表示,但并非所有用六方格子表示的结构都可以用三方格子表示。
到目前可能已经注意到了图 2-4(2) 中的结构与将 FCC 的方向,即以 <111>方向视为 c 轴,并垂直于该面堆叠层非常相似。实际上,属于立方晶系的简单立方格子、FCC 以及 BCC 都可以看作是斜方格子的一种,或者更准确地说,它们的基本平移向量在三方格子(晶格常数为a = b = c,α = β = γ)中具有特别高的对称性(γ = 90°,60°,109.47°)。从这个意义上说,在比较原子层的堆积结构时,可以将立方晶体也表示为六方格子,这样更容易理解。特别是对于 FCC,三方格子的基本平移向量长度与原来的六方网格的基本平移向量长度相等,图 2-4(3) 底面的三个黑点及其正上方的红点形成正四面体结构。今后,在考察晶体结构作为最密堆积层的堆积时,我们将立方晶的<111>方向与六方晶的<0001>方向对应起来,并在六方格子的 c 轴垂直的平面内,根据上下层的关系,将原子最密堆积可能的位点如图 2-4 所示标记为 A 位点、B 位点和 C 位点。
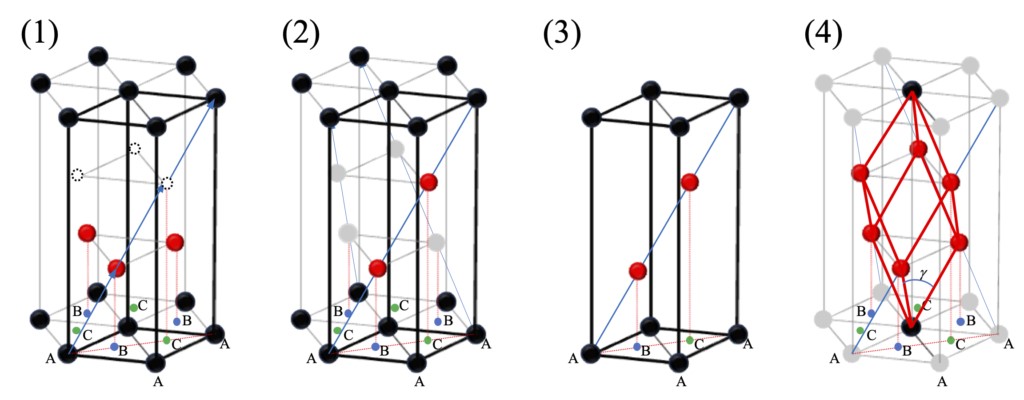
图 2-4 以六方棱柱为基础绘制的六方格子和斜方格子之间的关系,(1) 简单的六方格子,(2) 斜方晶格(复合六方格子),(3) 只取出(2)的单元格,(4) 重构为基础三方格子的三个斜方格子。在(2)、(3)和(4)中,黑圈和红圈中的原子位置为晶格点。图中的符号 A、B 和 C 表示垂直于 c 轴的平面上的位置,在这些位置上原子有可能紧密地排列在上层和下层之间。在 (4) 中,当 γ = 90˚、60˚ 和 109.47˚ 时(取决于 c 轴长度),晶格分别为简单立方格子、FCC 格子和 BCC 格子。
基于HCP的半导体晶体(GaN, SiC等)
回顾半导体材料技术的发展,直到 1990 年左右,Si 和 GaAs 等立方晶晶体仍是主导技术。当时的认识认为立方晶以外的晶体不可能作为半导体实际应用。GaN 和 SiC 等六方晶半导体晶体技术的发展颠覆了这一常识。
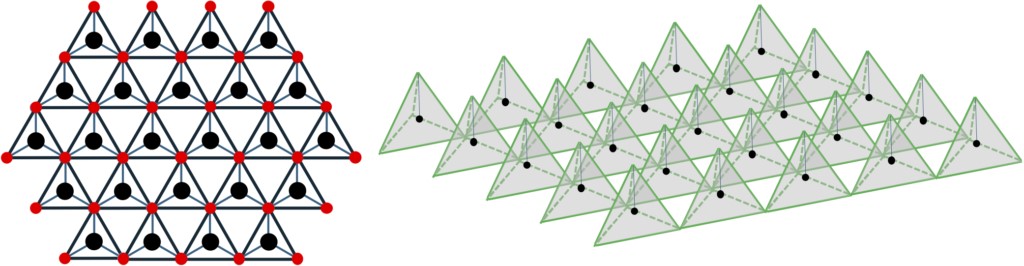
图2-5 将原子位于重心的正四面体结构以二维方式进行最密集填充配置的层结构。左图为平面图。右图为俯视图。
在基于 HCP 的半导体晶体中,与基于 FCC 的晶体一样,四面体结构也是形成晶体的基本结构。考虑在重心处配置原子的四面体结构(参照图2-5)的最密集填充配置的二维层沿 c 轴方向依次堆叠的结构时,如果将中心原子所在的最密集填充站点设为 A 点,则可以配置上层原子的最密集填充的 B 或 C 点。可以看出在 c 轴方向上排列该位置时,在基于 FCC 的闪锌矿型(GaAs)的情况下为ABCABC的堆叠模式,在基于 HCP 的纤锌矿型(GaN)的情况下为 ABAB 的堆叠模式。如图 2-6 所示,堆叠的层为最密充填结构,这里考虑包含位于与上层之间的空穴中不同原子的一层。六方网格的基本单元晶胞用图中的黑色实线表示,同时展示了由格点原子 1 和位于空隙中的原子 2 组成的元素结构。从该图的单元晶胞内的平面来看,原子 1 的位置对应 A 点,原子 2 的位置对应B点,而原子 2 右上方的空隙位置对应 C 点。
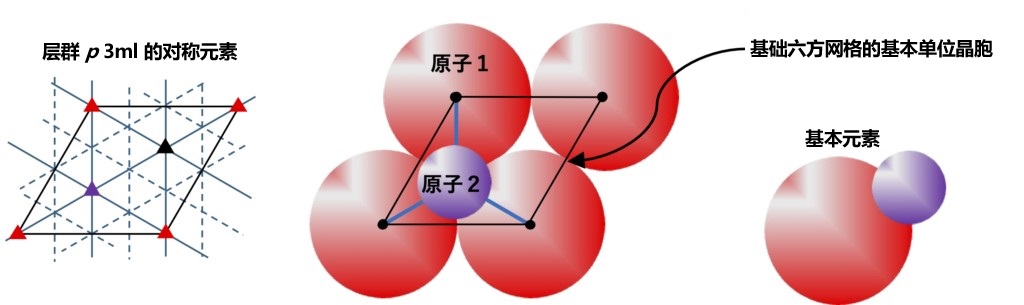
图2-6 基础六方网状单胞和紧密堆积层中的基本元素。原子键合用蓝线表示。此外,从原子 1 到图的背面和从原子 2 到图的正面还分别有一条原子键。该层结构所属层组(p 3m1)的对称元素如左图所示。在左图中,红色三角形位置对应 A 点,紫色三角形位置对应 B 点,无原子的黑色三角形位置对应 C 点
现在,让我们将图 2-6 中的层沿着垂直于纸面的 c 轴方向堆叠起来。由于键合方位的限制,层与层之间需要进行平行移动。这种情况下,在第 1 层上方的第 2 层中,原子 1 只能被放置在 B 点上。进一步地,在第 3 层中,原子将被放置到 C 点上。这种排列即所谓的 “ABCABC” 排列,也就是闪锌矿型结构的典型特征。这种堆叠情况意味着,第1层的晶格在层内以 (1/3, 1/3) 的方式平移堆叠。同时,这种平移在 c 轴方向上再加上 1/3,从而在空间中形成了 (1/3, 1/3, 1/3) 的平移矢量。这实际上反映了斜方晶格的形成。这种斜方晶格的形成来源于最密充填结构的特性,其中的 3 个平移矢量具有相等的长度,并且矢量之间的夹角为 60˚。这一几何关系决定了这种斜方晶格可以被归类为 FCC(面心立方)结构。
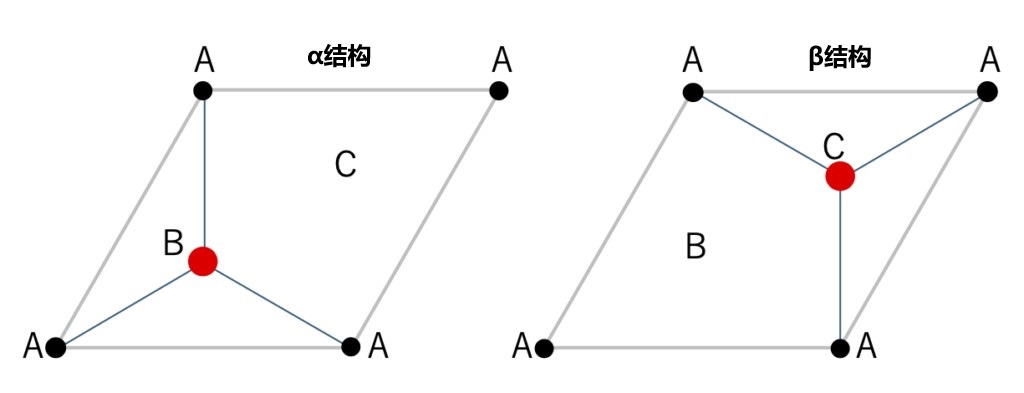
图 2-7 包括元素结构的二维紧密堆积结构,及其 180˚ 旋转(均属于层组 p 3m1)的示意图。左图的结构为 α 结构,右图的结构为 β 结构。
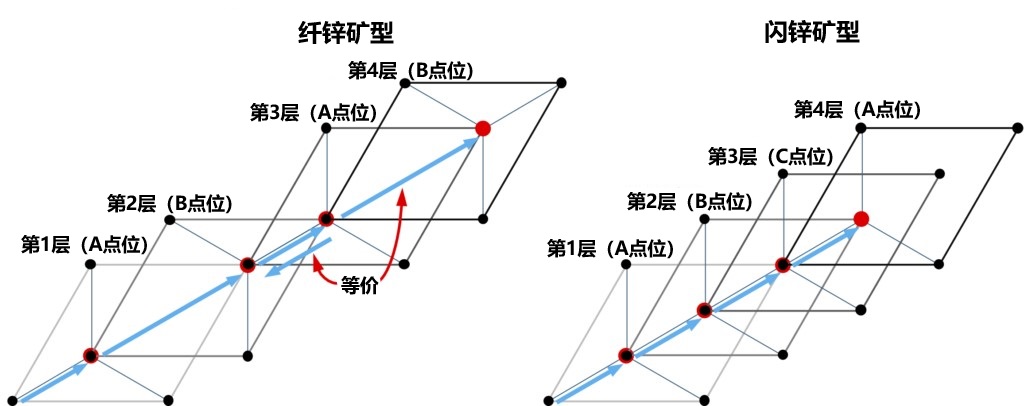
图 2-8 包括元素结构在内的二维紧密堆积结构在 c 轴方向上的堆积,其平面内移动方向为 [-1010](右上角的蓝色箭头与 Zhdanov 符号中的正方向相对应)。在闪锌矿类型中,所有层在α结构中通过(1/3,1/3)有规律地移动(1/3,1/3),而在纤锌矿型中,α 和 β 结构交替堆叠,在 α→β 中为(1/3,1/3),在 β→α 中为(2/3,2/3)(相当于β→α中的(-1/3,-1/3))。
如上述内容所描述,仅通过平行移动最密堆积层进行堆叠时,只能生成 FCC 结构。那么,关于如何构造出 HCP 结构,如图 2-7 所示,需要将原始最密堆积层与其旋转 180°(由于层具有三重旋转轴,旋转 60° 或 300° 在几何上是等价的)的结构交替堆叠。在图 2-6 右侧所示的包含基本要素的最密堆积层中,并不存在二重旋转轴或六重旋转轴的对称操作,因此,图 2-7 中的两种层结构无法仅通过平行移动重合。这意味着,在堆叠第二层时,不仅需要调整晶格点的位置,还需要将整个层旋转 180°。图 2-8 展示了两种层结构交替堆叠的过程。此外,从<11-20>方向观察由正四面体排列组成的晶体,可以清晰地看到层的 180° 旋转(图2-9)。将这两种层结构分别称为 α 结构和 β 结构。无论是 α 结构还是 β 结构,其上层的晶格点位置都具有唯一性的决定于自身层中原子 2 的位置。这意味着堆叠过程中,晶格点的排列顺序和层结构是紧密相关的。也就是说,在基础层上方,α 结构的堆叠顺序为 A→B→C→A→,而 β 结构的堆叠顺序为 A→C→B→A→。对于 FCC(闪锌矿型)结构,堆叠仅由 α 结构组成,A、B、C 三种晶格点以 1/3 的比例顺序均匀排列;而 HCP(纤锌矿型)结构的形成则需要 α 结构和 β 结构交替排列。如果将位序和层结构作为一个整体来表示,FCC 可以描述为“ABCABC…”,而 HCP 可以描述为“AB'AB'”(其中“'”表示 β 结构)。这种表述方式更容易理解。但在 HCP 中,临近的两层之间丧失了平移对称性,同时晶格点和结构呈一一对应的关系。在由正四面体结构组成的层的堆叠中,关键点在于层结构的转换发生在何处,以及这种转换发生的频率。此外,在 HCP 中,C 点处于空位状态,因此与 A 和 B 点不再等价。这种情况构成了 FCC 和 HCP 晶体结构之间的主要区别。
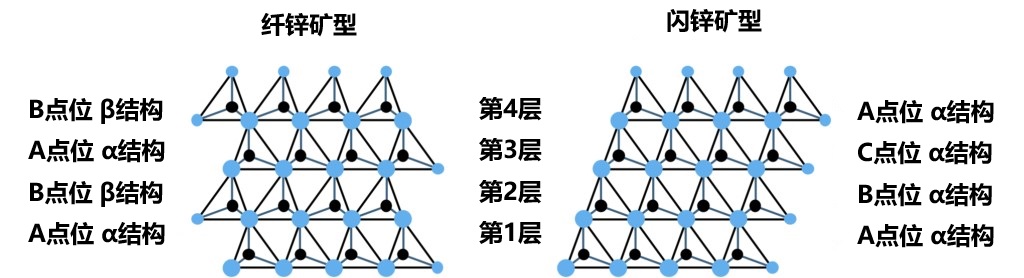
图 2-9 从六方格子- <1120> 方向看纤锌矿型和闪锌矿型结构中四面体结构的排列。图中显示了各层的位点位置和层结构。
接下来,我们从垂直方向对比由堆叠形成的闪锌矿型晶体的 {111} 面和纤锌矿型晶体的 {0001} 面的对称性。两种结构的最密堆积位置和主要对称元素如图 2-10 所示。在基本的六方格子中,晶格点位置(A点)两者均具有三重旋转轴。然而,对于 B 点和 C 点,这两种结构之间存在显著差异。在闪锌矿型晶体中,B 点和 C 点均存在三重旋转轴;而在纤锌矿型晶体中,B 点具有三重旋转轴,但 C 位置(没有原子存在)却形成了具有 63 的六重螺旋轴。此外,在闪锌矿型晶体中,最密堆积位置有三种类型,对应地,三重螺旋轴规则地出现在围绕这三种最密堆积位置的单位晶胞中。而在纤锌矿型晶体中,三条二重螺旋轴仅围绕 B 位置出现。通过这样的比较,可以得出结论:闪锌矿型晶体相比纤锌矿型晶体具有更高的对称性。
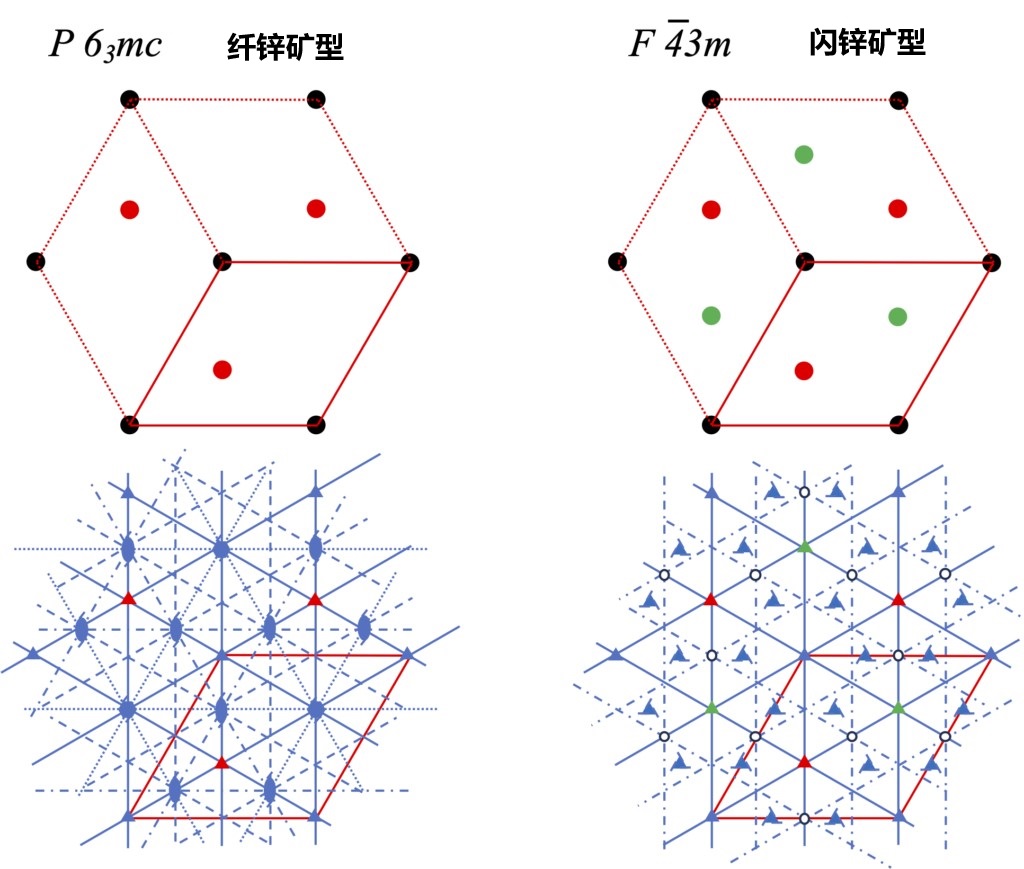
图 2-10 垂直于纤锌矿型晶体{0001}面和闪锌矿晶体{111}面的原子构型和对称元素。红色方框表示六方格子中的单位晶胞,黑色圆圈表示 A 点上的原子,红色圆圈表示 B 点上的原子,绿色圆圈表示 C 点上的原子。
在认识到差异后,让我们思考一下外延薄膜从衬底结构向上层传递时的结构变化情况。正如之前所述,正四面体结构以及化学键的取向在其中发挥了重要作用。图 2-11 中展示了生长过程中最表面原子的结合状态。如同有机化学中广为人知的那样,由 sp3 共价键形成的正四面体之间的结合由于立体位阻的原因,图 2-11 中所示的 α 结构排列被认为更稳定。在最表面层中,当原子 2 的键合方向确定后,在这之上正在形成的层更容易趋向于形成 α 结构排列。然而,正在形成的层中,由于原子 1 向上延伸的结合键与其连接上方原子 2 的键合尚未完成,因此方向并未固定。在这种情况下,可以与最表面原子 2 之间结合为轴自由旋转,这正是外延生长过程中 β 结构产生的机制。可以认为,由稳定性更高的 α 结构排列形成的结构是闪锌矿型结构,其特征是三个等价的最密堆积位点的规则排列。而在纤锌矿型结构中,由于 C 点为空位,如果此处原子由奇怪的方式进入的话,将会引发晶体缺陷。此外,作为 C 点对称元素的三重旋转轴仅在该层内完成原子排列信息的传递,而六重螺旋轴则受到 c 轴方向平移对称性的影响,只有上下层信息准确传递时才能成立。外延生长是衬底的结构信息向上层传递的现象,但在传递到形成中的上层时,传递距离越长,自然产生错误的概率也会越高。进一步而言,如果在形成中的层中正四面体已经相互结合并使得层形成完毕,那么原子 1 和原子 2 之间的平面会成为晶体中的滑移面。在这种情况下,C 位点如果存在原子,从另一个角度看,就与所谓的“Shockley 型堆积断层”相同。由此看来,纤锌矿型结构中,部分最密堆积位点为空位,且此处存在的旋转对称元素为螺旋轴,因此在晶体生长过程中 C 点原子填入的可能性较高,可以被视为一种生长中的错误。
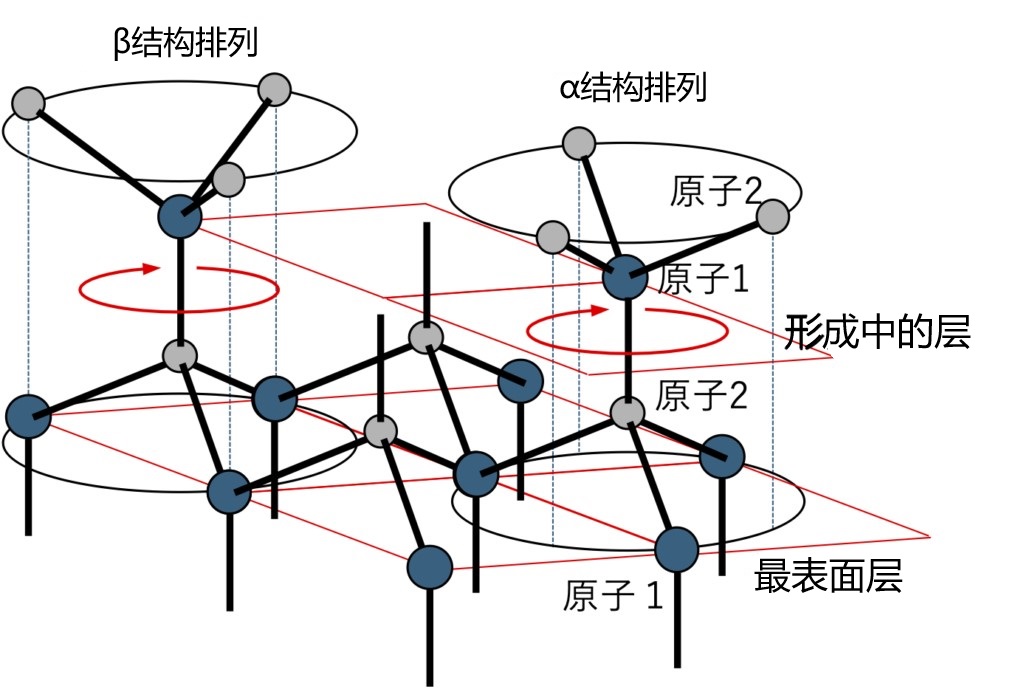
图 2-11 生长顶部表面的化学键合。图中箭头所示的旋转运动可能发生在形成层中:在 β 结构中,键合的方向相对于 α 结构旋转了 180˚;在 β 结构中,形成层中原子 2 的位置与最顶层中原子1的位置重叠,但在 α 结构中没有重叠;在 α 结构中,形成层中原子 1 的位置与最顶层中原子 2 的位置重叠,但在 β 结构中没有重叠。
截止到目前,我们将 HCP 结构中 C 点存在原子的情况视为一种导致晶体缺陷的错误。然而,如果在 “ABAB...” 的堆叠顺序中,C 点的原子以规则的形式出现,会出现什么情况?事实上,这种现象实际上在 SiC(碳化硅)晶体的多形(晶体多型)中已经被观察到了。在 SiC 中,代表性的晶体多形包括 4H、6H、3C(根据 Ramsdell 记号法)。这些多形的堆叠结构如图 2-12 所示。这些堆叠结构本身并非 SiC 特有的,为了进行比较,使用Zhdanov记号法非常方便。例如,3C 被表示为(1)或(∞),2H 为(1 -1),4H 为(2 -2),6H为(3 -3)。在这种记号法中,沿着 c 轴方向,连续 α 结构的堆叠数用正整数表示,连续 β 结构的堆叠数用负整数表示,括号中的数字表示重复单元。可以非常直观的看出正负整数交界处表示层结构的切换。从空间群的角度来看,2H、4H 和 6H 的空间群是相同的。然而,从层与层结构切换的角度来看,3C 和2H 分别处于两个极端,具有某种明显的规律性。在 3C 结构中,层结构完全没有切换;而在 2H 结构中,每一层都会发生切换。4H 和 6H 结构则位于两者之间。为了表示切换程度,存在一个名为“Hexagonality” 的概念,用来定量描述层结构切换的频率(4H 为 50%,6H 为 33%)。
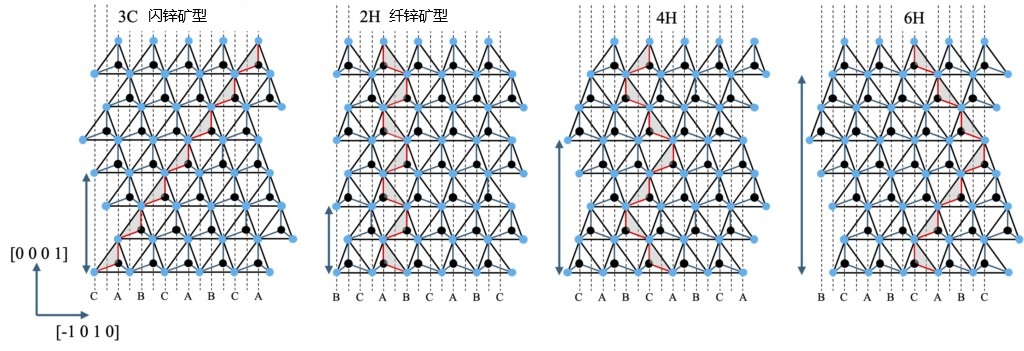
图 2-12 层结构(p 3m1)沿 c 轴方向周期性堆叠的晶体结构,其中 3C 为 "ABCABCA....” 2H 为"ABABA....” 4H为 "CACBC....” 6H 为 "CABCBAC....” 以下是示例。在图中的2H、4H 和 6H 中,C 点与其他两个位点的特征不同。红线和带帽连线位于同一的{11-20}平面上。各图左边的箭头表示 c 轴长度。
从上述的 Zhdanov 记号法来看,与 3C 相比,2H、4H 和 6H 的层叠结构可以理解为在生长过程中的一种“错误”,即堆叠结构在生长中发生了转换。这种转换以周期性的形式出现,例如每一层、每两层或每三层发生一次转换。这种 c 轴方向的周期性必须通过宏观尺度的晶体生长得以保持,而实现这种保持的关键机制正是外延生长。在外延生长技术中,衬底的信息需要被准确地传递到生长表面,以确保周期性的结构能够被忠实地再现。然而,当 c 轴方向的周期变长,衬底信息的传递会变得困难,导致上层外延层中难以实现准确的再现堆叠结构。这意味着,随着周期性延长,信息传递的准确性和生长过程的稳定性都会受到限制。
另一方面,如果层结构的转换不是周期性的,那么就会形成局部的“堆叠缺陷”。例如,在 4H-SiC 晶体(Zhdanov 表记为 (2 2))中,已发现存在两种典型的 “Single Shockley 型”和 “Double Shockley 型”堆叠缺陷。这些缺陷分别可以用 (3 -1) (ABA’C’ →ABCB’)和 (6 -2) (ABA’C’ABA’C’ → ABCABCB’A’)来表示。这些缺陷可能存在于晶体中 c 轴方向的某些区域,因为它们与母体 4H-SiC 的 4 层周期非常匹配。然而,这些堆叠缺陷上方的 4H-SiC 区域会因为缺陷的存在导致堆叠的不连续性,正如图 2-13 所示。这些缺陷会破坏晶体的层叠规则性,使得 c 轴方向的平移对称性丧失。
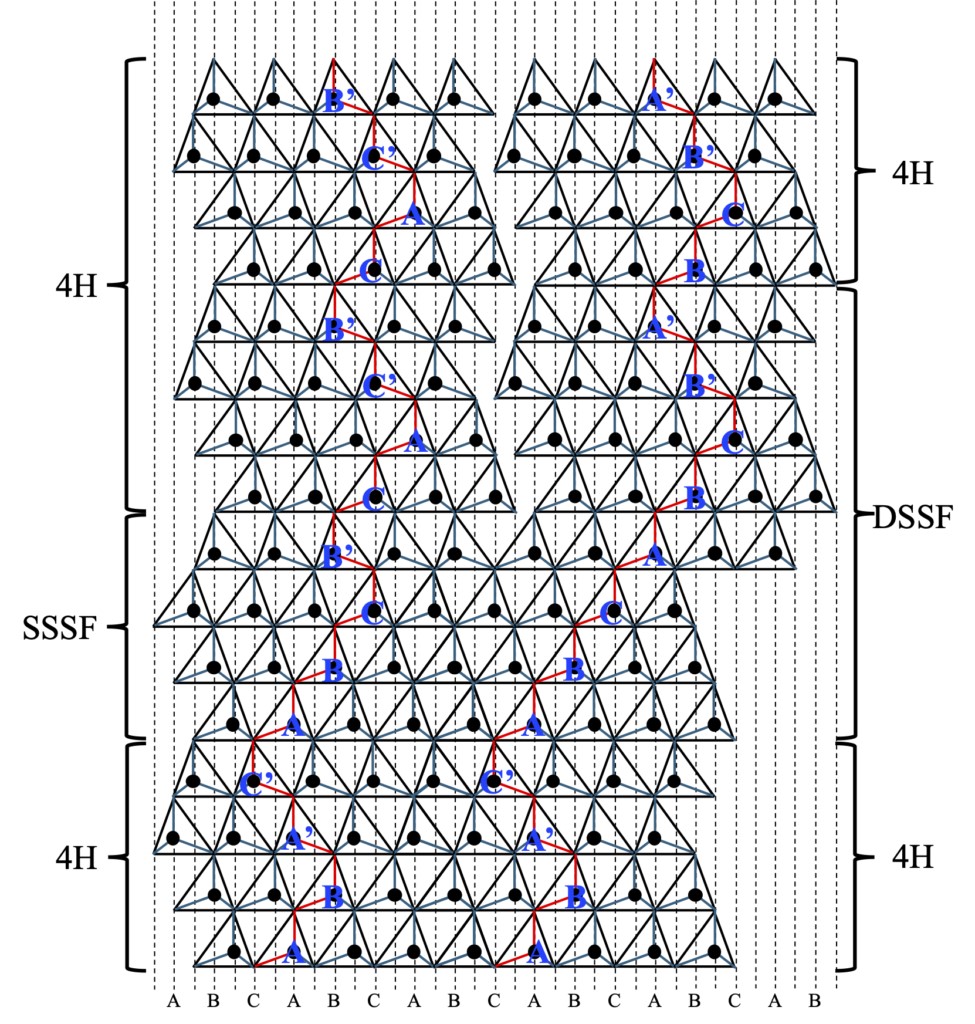
图 2-13 4H-SiC 中Single Shockley 型堆叠缺陷(SSSF)和Double Shockley型堆叠缺陷(DSSF)的堆叠情况。上层恢复了 4H-SiC 的周期性堆叠结构,但原子占据的位点与底层不同,相互之间的堆叠关系不规则。
在本章内容中,我们针对以 HCP 为基础的晶体,对其由最密堆积层的层叠结构所构成的晶体特征和形成方式进行了整理和分析。在下一章,将讨论由于层叠结构的差异对晶体系统所造成的影响,以及因此产生的以三方晶系菱面体晶格为基础的晶体和单斜晶系晶体。
参考文献
北野保行、電子顕微鏡, Vol.29, No.2, pp.118-123 (1994).
Appendix 2
· 堆叠结构的表示方法
(1) Ramsdell记号:NSn
· N:一个周期(即晶胞)内的堆叠层数。
· S:晶胞的对称性(C:立方晶,H:六方晶,R:三方晶)
· N:同一组内 NS 相同的情况下,用作区分的连续编号,通常可以省略。
(2) Zhdanov记号:(m -n . . . . . . .)k
· M:沿正方向均匀移动的堆叠层数
· -n:沿反方向均匀移动的堆叠层数
· . . . . :不同m -n对的重复
· K:在晶胞中(m n . . . . . . .) n 结构的重复次数,如为 1 则省略。
· 如果 k = 1 且结构清晰,也可简单表示为 n。
(3) c-h sequence:c, h
一种描述单周期堆积结构的方法,其中层结构(α-结构或β-结构)相对于最近被替换的层用 h(hexagonal)代替,未被替换的层用 c(cubic)代替。例如,3C为c,2H为h,4H为ch,6H为cch。


