【国内论文】中山大学王钢教授团队：异质外延ε-Ga₂O₃薄膜的热膨胀特性研究

        由中山大学王钢教授、陈梓敏副教授的研究团队在学术期刊 Advanced Engineering Materials 发布了一篇名为 Investigation on the Thermal Expansion Property of ε-Ga₂O₃ Thin Films Grown by Heteroepitaxy（异质外延 ε-Ga₂O₃ 薄膜的热膨胀特性研究）的文章。

        这项工作得到了以下项目的支持：国家重点研发计划（项目编号：2023YFF1500700）、国家自然科学基金（项目编号：62074167）、广东省重点研发计划项目（项目编号：2021B0101300005）、广东省基础与应用基础研究基金（项目编号：2022B1515120081）。

        近年来，ε-Ga₂O₃（κ-Ga₂O₃）作为 Ga₂O₃ 家族的重要亚稳相，因其超宽禁带（≈4.9 eV）、显著的自发极化以及强压电效应而备受关注，在高电子迁移率晶体管和射频前端滤波器件等领域展现出应用潜力。然而，由于 ε-Ga₂O₃ 缺乏体材料，其生长只能依赖异质外延，这使得应力控制成为制约其发展的关键问题。异质外延过程中不可避免的晶格失配与热失配，若得不到有效调控，将导致薄膜开裂、翘曲，严重影响器件性能与可靠性。尽管其晶体结构和晶格常数已通过理论与实验得到确认，但热膨胀特性仍未明确，这阻碍了应力调控与外延工艺优化的深入研究。因此，开发适用于 ε-Ga₂O₃ 及其他薄膜材料体系的热膨胀系数测量方法，具有重要的科学意义和应用价值。

        新型功能材料与器件的快速发展带来了更为严峻的材料生长挑战。其中，应力工程在从材料生长、器件制造到封装的全过程中都具有重要影响。本文研究了 ε-Ga₂O₃ 薄膜的残余应力，采用温度依赖的高分辨率X射线衍射（HRXRD）ω 扫描进行曲率测量，结果显示在所有 ε-Ga₂O₃ 样品中均观察到较高的张应力。结合 Stoney 方程，首次提取出 ε-Ga₂O₃ 的热膨胀系数：在（001）面内为 10.8–11.2 × 10^-6 °C⁻¹，在垂直于（001）面方向为 5.03–7.66 × 10^-6 °C⁻¹。由于热失配存在显著差异（与 Si 的失配达 209%，与蓝宝石为 54%），厚度 700 nm 的 Si 衬底 ε-Ga₂O₃ 出现裂纹。本研究不仅为 ε-Ga₂O₃ 的应力调控提供了依据，同时提出了一种适用于薄膜材料异质外延体系的通用热膨胀系数测量方法。

        本文研究了宽禁带半导体 ε-Ga₂O₃ 薄膜异质外延的热失配特性。对于生长在 c 面蓝宝石基底和 Si(111) 基底上的样品，均观测到较高的张应力。利用 HRXRD ω 扫描结合双层结构模型（ε-Ga₂O₃/蓝宝石）和三层结构模型（ε-Ga₂O₃/AlN/Si(111)），开展了温度对残余应力的影响。结果表明，ε-Ga₂O₃ 在 (001) 面内的双轴热膨胀系数 α_‖ε-Ga2O3 为 10.8–11.2 × 10^-6 °C^-1，而垂直于 (001) 面的热膨胀系数 α_⊥ε-Ga2O3 为 5.03–7.66 × 10-6 °C⁻¹。相应地，ε-Ga₂O₃ 在蓝宝石上的热失配为 54%，在 Si 上的热失配则高达 209%。在厚度为 700 nm 的 Si 基 ε-Ga₂O₃ 薄膜中观察到裂纹，而厚度为 1800 nm 的蓝宝石基薄膜中未见裂纹，进一步表明 ε-Ga₂O₃ 与 Si 之间存在更大的热失配。精确测定的热膨胀系数不仅揭示了 ε-Ga₂O₃ 的基本热膨胀特性，也为其外延应力调控提供了关键指导。

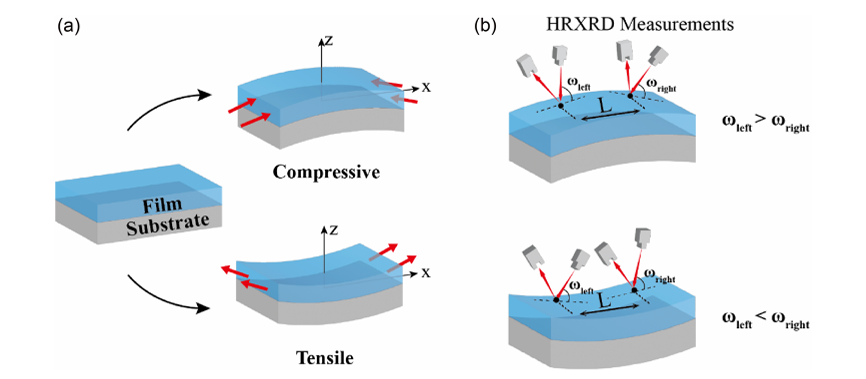
图 1. a) 外延薄膜与基底之间的应力状态可能导致晶圆翘曲。b) 离位 HRXRD 曲率测量模型。L 表示 ω 扫描测量中两点之间的水平距离。曲率由 κ=1/ R≈(ω_r-ω_l)/|L|确定。

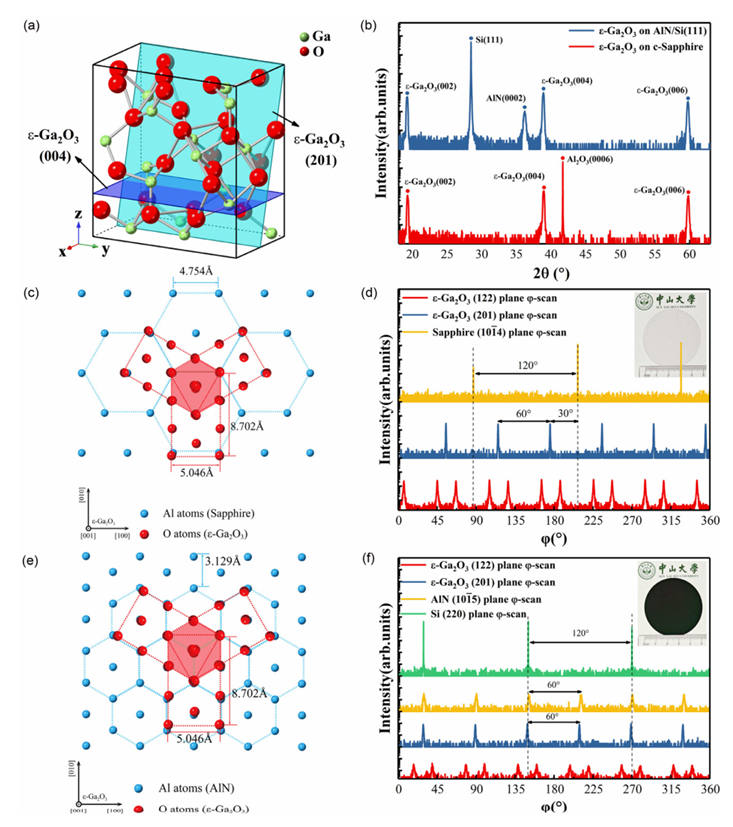
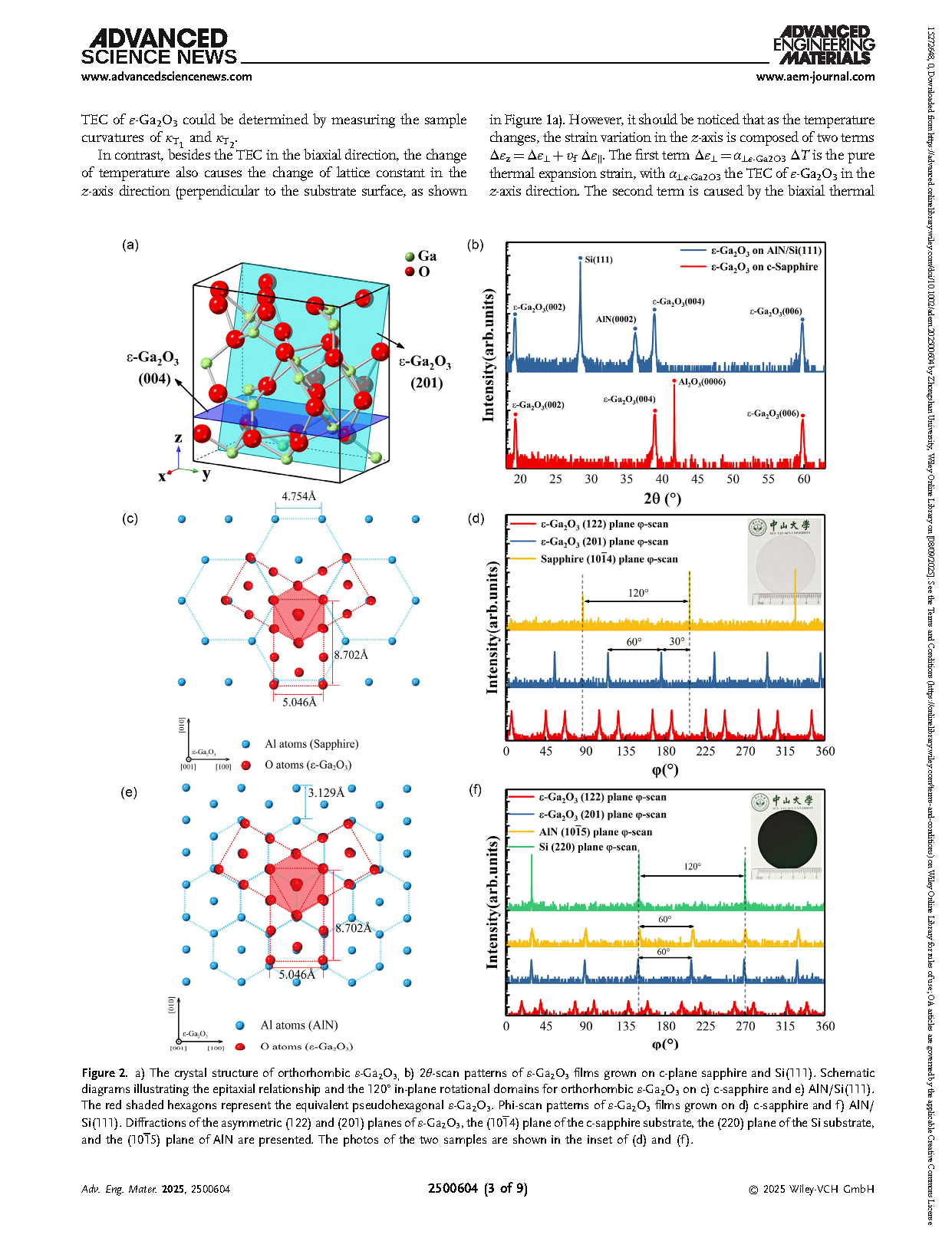
图 2. a) 正交晶系 ε-Ga₂O₃ 的晶体结构；b) 生长在 c 面蓝宝石和 Si(111) 基底上的 ε-Ga₂O₃ 薄膜的 2θ 扫描图；c) ε-Ga₂O₃ 在 c 面蓝宝石上的外延关系与 120° 面内旋转畴示意图；e) ε-Ga₂O₃ 在 AlN/Si(111) 上的外延关系与旋转畴示意图。红色阴影六边形表示等效的准六方 ε-Ga₂O₃；d) 生长在 c 面蓝宝石上的 ε-Ga₂O₃ 薄膜的 φ 扫描图；f) 生长在 AlN/Si(111) 上的 ε-Ga₂O₃ 薄膜的 φ 扫描图。图中给出了 ε-Ga₂O₃ 的非对称 (122) 和 (201) 衍射峰、c 面蓝宝石衬底的 (10-14) 衍射峰、Si 基底的 (220) 衍射峰以及 AlN 的 (10-15) 衍射峰。(d) 和 (f) 插图为两种样品的实物照片。

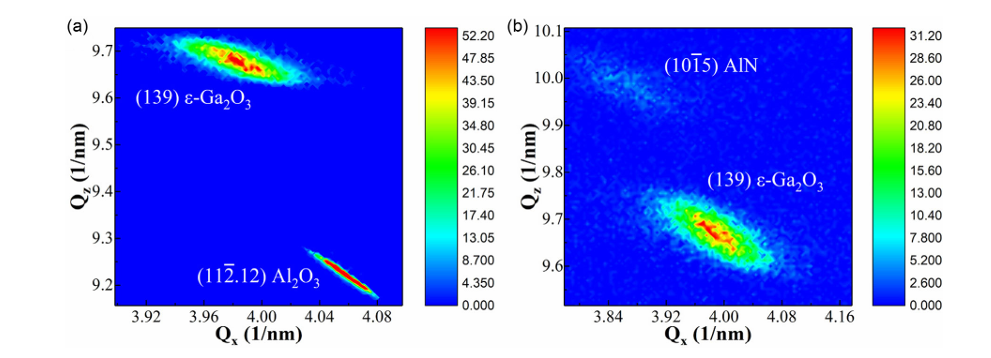
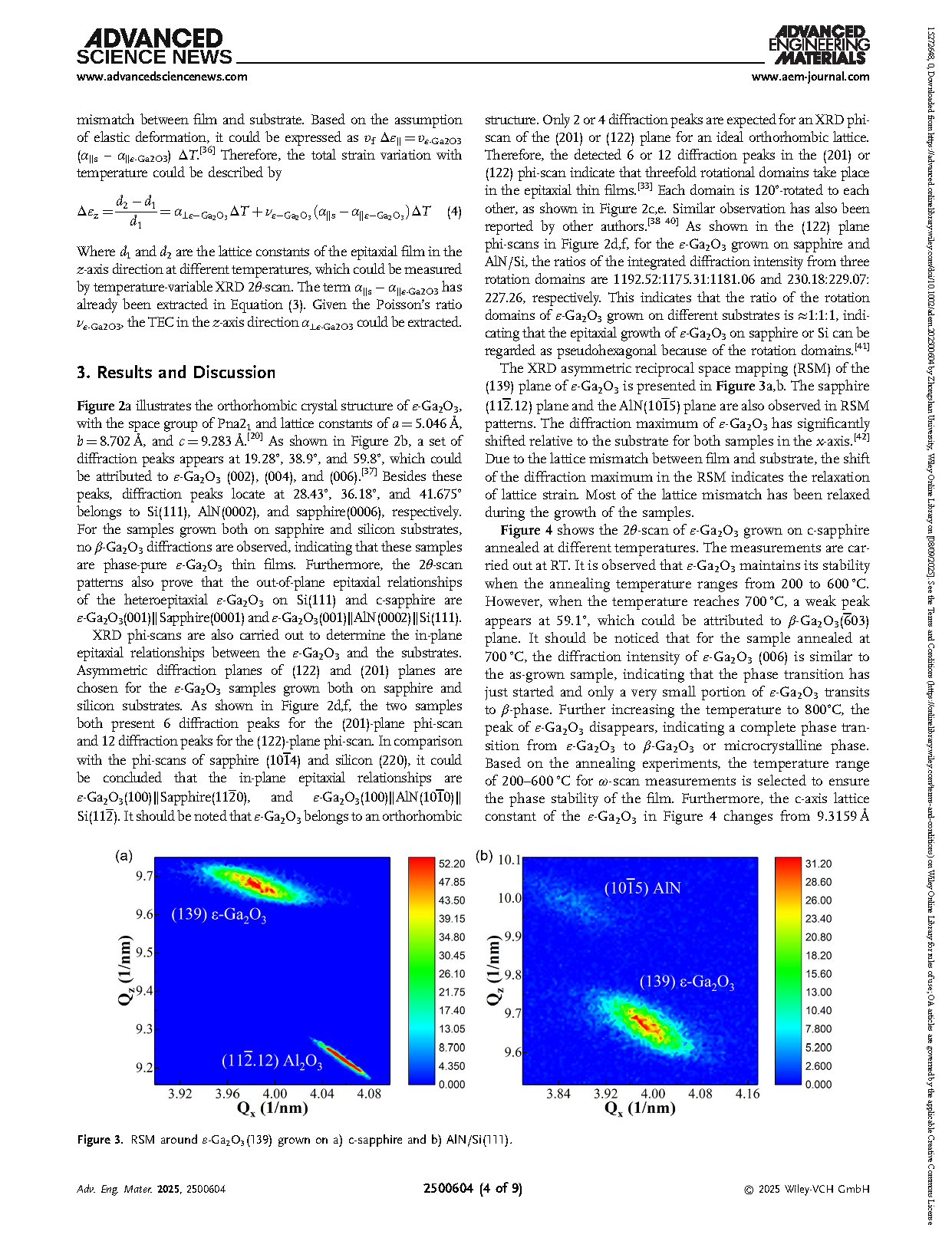
图 3. a) 生长在 c 面蓝宝石上的 ε-Ga₂O₃ (139) 的倒易空间图 (RSM)；b) 生长在 AlN/Si(111) 上的 ε-Ga₂O₃ (139) 的倒易空间图。

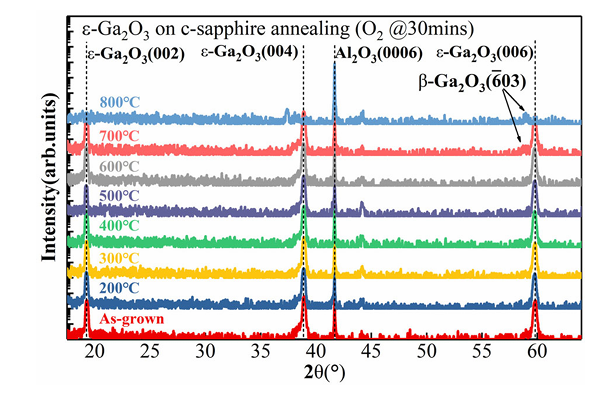
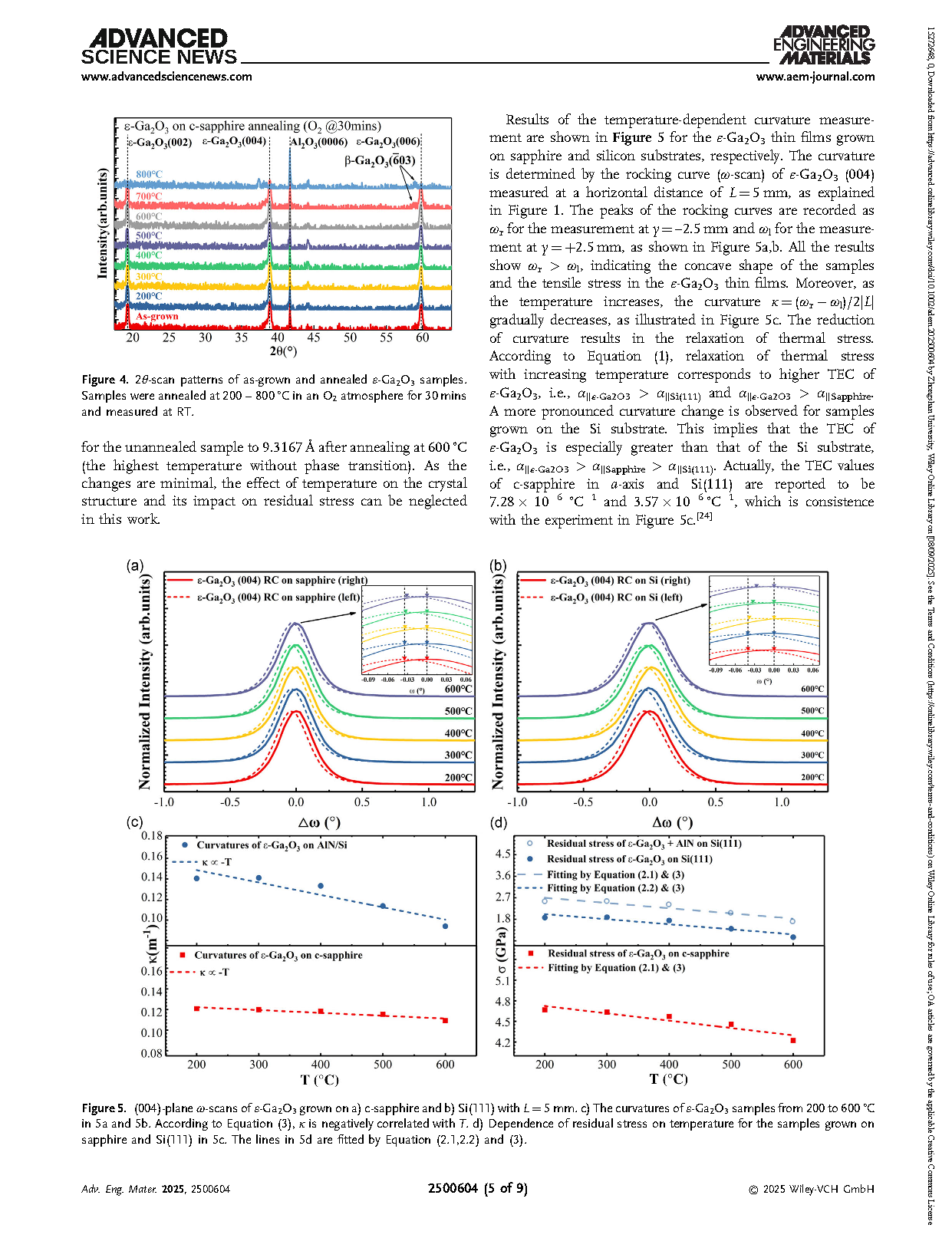
图 4. 原始态与退火处理后的 ε-Ga₂O₃ 样品的 2θ 扫描图。样品在 O₂ 气氛下于 200–800°C 退火 30 分钟，并在室温 (RT) 下测量。

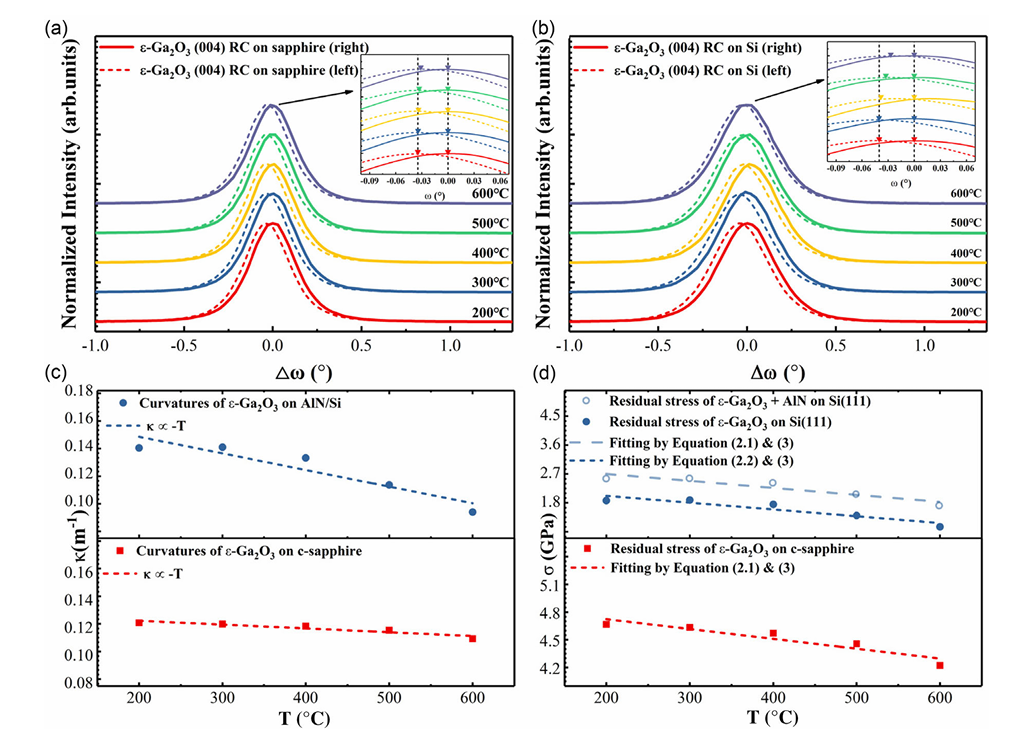
图 5. a) 生长在 c 面蓝宝石上的 ε-Ga₂O₃ (004) 晶面 ω 扫描 (L=5 mm)；b) 生长在 Si(111) 上的 ε-Ga₂O₃ (004) 晶面 ω 扫描 (L=5 mm)；c) 对应 a 和 b 样品在 200–600°C 范围内的曲率变化。根据公式 (3)，κ 与温度 T 呈负相关；d) 蓝宝石基和 Si 基 ε-Ga₂O₃ 样品的残余应力随温度的变化关系。5d 中的曲线分别由公式 (2.1, 2.2) 和 (3) 拟合。

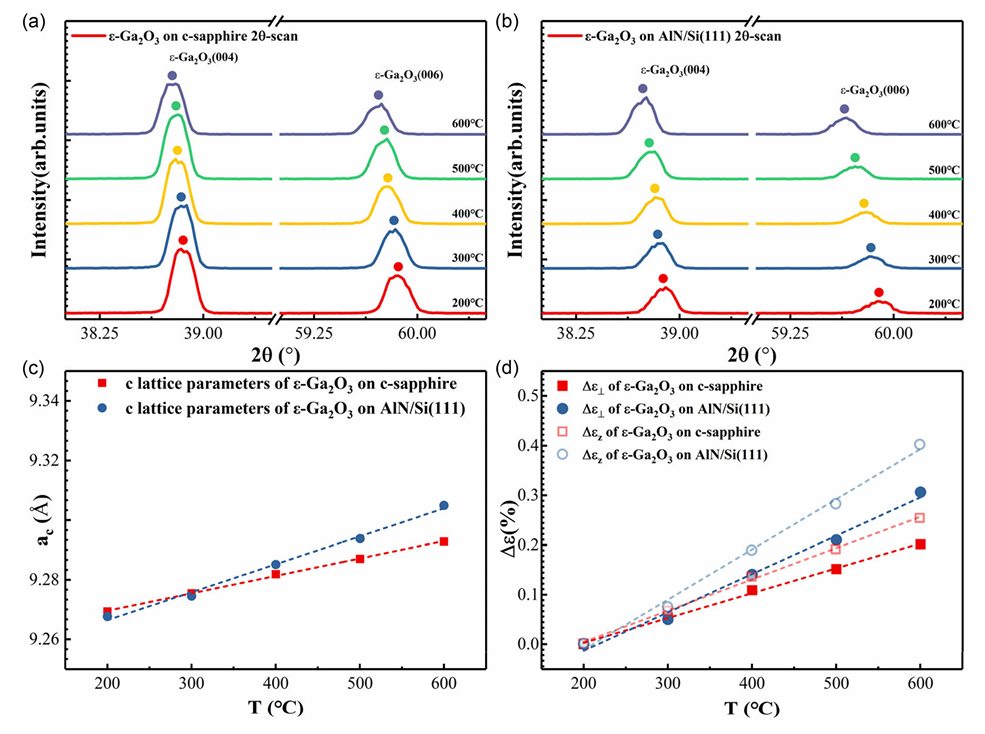
图 6. a) 生长在 c 面蓝宝石上的 ε-Ga₂O₃ 在 200–600°C 的 2θ 扫描；b) 生长在 Si(111) 上的 ε-Ga₂O₃ 在 200–600°C 的 2θ 扫描；c) 根据布拉格定律 (2d sinθ=nλ)，由 a 和 b 图提取的 ε-Ga₂O₃ 外延薄膜的晶格参数 ac。图中直线仅作视觉参考；d) 基于 c 图中晶格参数，ε-Ga₂O₃ 在 200–600°C 的 z 方向应变变化。6c 中的曲线依据公式 (4) 拟合，即 Δε_⊥=Δε_z- υ_ε-Ga2O3 (α_‖s- α_‖ε-Ga2O3) ΔT。

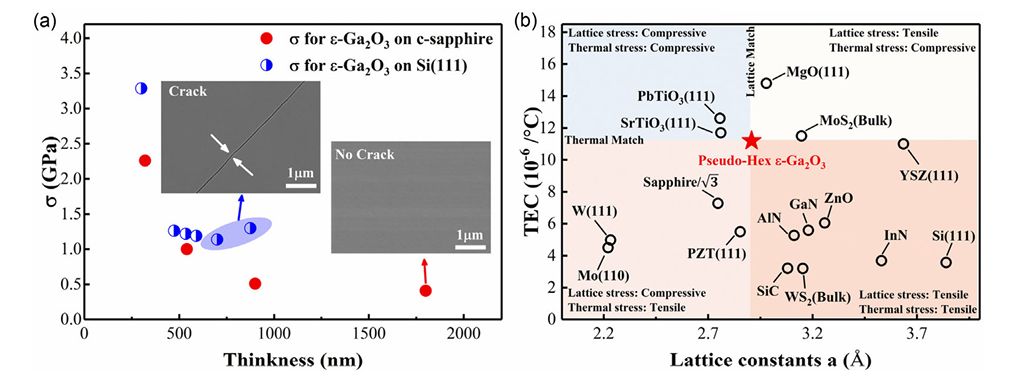
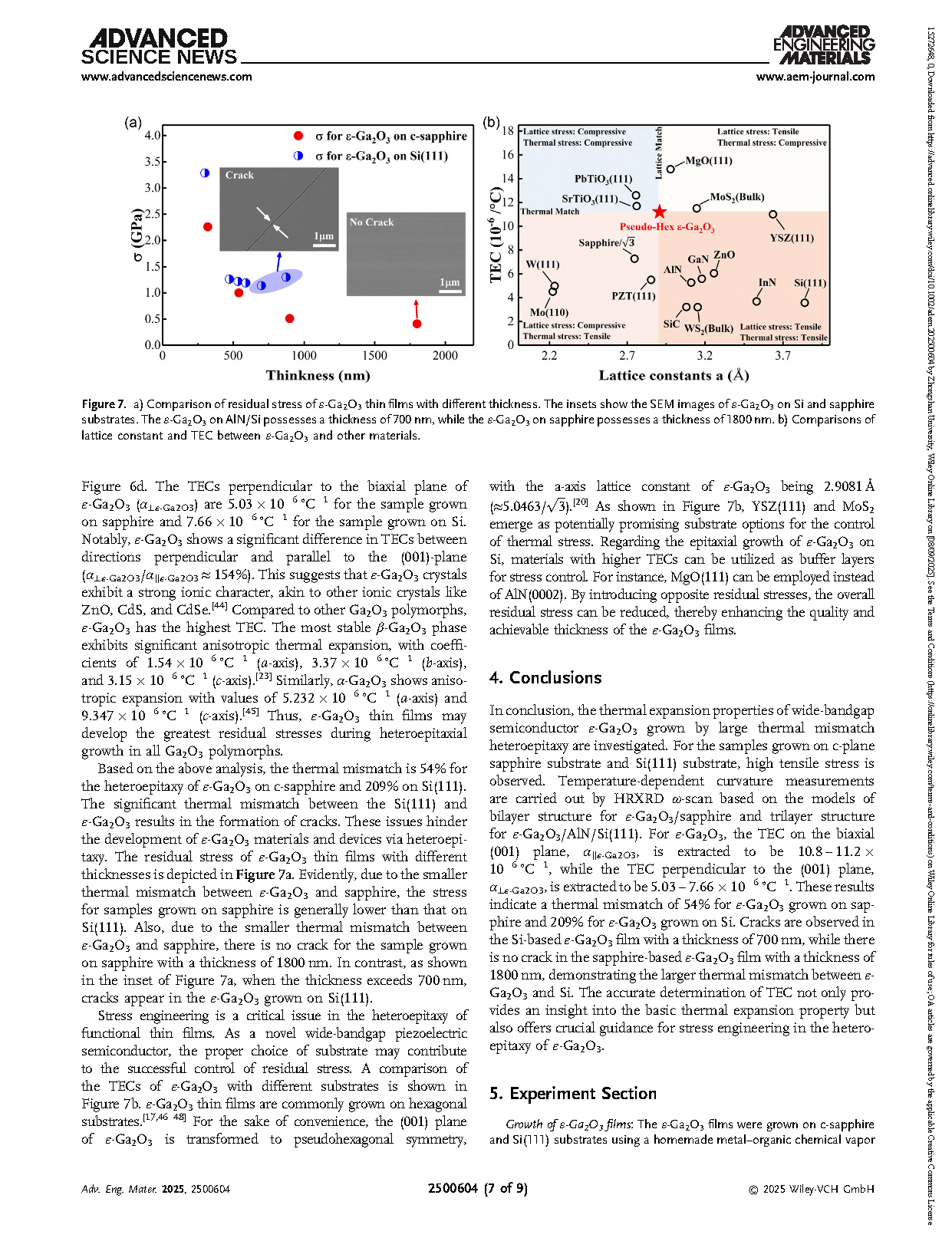
图 7.a) 不同厚度 ε-Ga₂O₃ 薄膜的残余应力对比。插图为 ε-Ga₂O₃ 在 Si 基和蓝宝石基上的 SEM 图像。 ε-Ga₂O₃/AlN/Si 的厚度为 700 nm，而 ε-Ga₂O₃/蓝宝石的厚度为 1800 nm；b) ε-Ga₂O₃ 与其他材料的晶格常数及热膨胀系数对比。

DOI：

doi.org/10.1002/adem.202500604